Gaussian Mixture HMM

The Gaussian Mixture HMM is a variant of HMM that uses a multivariate Gaussian mixture model as the emission distribution for each state.

This HMM variant can be used to recognize unbounded real-valued univariate or multivariate sequences.

Emissions

The emission distribution \(b_m\) of an observation \(\mathbf{o}^{(t)}\) at time \(t\) for state \(m\) is formed by a weighted mixture of \(K\) multivariate Gaussian probability density functions, defined as:

\[b_m(\mathbf{o}^{(t)}) = \sum_{k=1}^K c_k^{(m)} \mathcal{N}_D\big(\mathbf{o}^{(t)}\ \big|\ \boldsymbol\mu_k^{(m)}, \Sigma_k^{(m)}\big)\]

Where:

  • \(\mathbf{o}^{(t)}=\left(o_1^{(t)}, o_2^{(t)}, \ldots, o_D^{(t)}\right)\) is a single observation at time \(t\), such that \(\mathbf{o}^{(t)}\in\mathbb{R}^D\).
  • \(c_k^{(m)}\) is a component mixture weight for the \(k^\text{th}\) Gaussian component of the \(m^\text{th}\) state, such that \(\sum_{k=1}^K c_k^{(m)} = 1\) and \(c_k^{(m)}\in[0, 1]\).
  • \(\boldsymbol\mu_k^{(m)}\) is a mean vector for the \(k^\text{th}\) Gaussian component of the \(m^\text{th}\) state, such that \(\boldsymbol\mu_k^{(m)}\in\mathbb{R}^D\).
  • \(\Sigma_k^{(m)}\) is a covariance matrix for the \(k^\text{th}\) Gaussian component of the \(m^\text{th}\) state, such that \(\Sigma_k^{(m)}\in\mathbb{R}^{D\times D}\) and \(\Sigma_k^{(m)}\) is symmetric and positive semi-definite.
  • \(\mathcal{N}_D\) is the \(D\)-dimensional multivariate Gaussian probability density function.

Using a mixture rather than a single Gaussian allows for more flexible modelling of observations.

The component mixture weights, mean vector and covariance matrix for all states and Gaussian components are updated during training via Expectation-Maximization through the Baum-Welch algorithm.

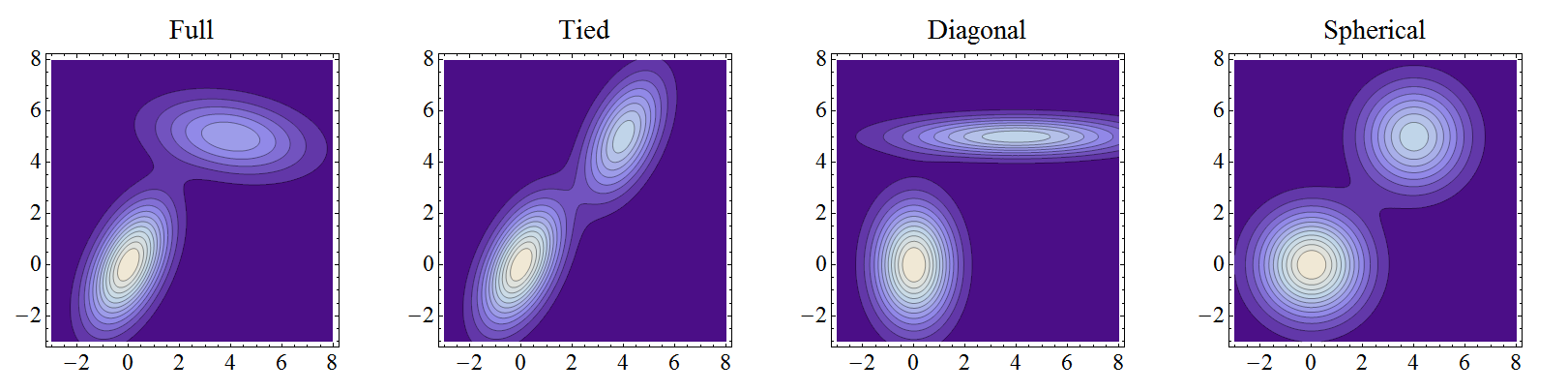
Covariance matrix types

The \(K\) covariance matrices for a state can come in different forms:

  • Full: All values are fully learnable independently for each component.

  • Diagonal: Only values along the diagonal may be learned independently for each component.

  • Spherical: Same as diagonal, with a single value shared along the diagonal for each component.

  • Tied: Same as full, with all components sharing the same single covariance matrix.

Estimating a full covariance matrix is not always necessary, particularly when a sufficient number of Gaussian components are used. If time is limiting, a spherical, diagonal and tied covariance matrix may also yield strong results while reducing training time due to having fewer parameters to estimate.

Covariance Types

API reference

Class

GaussianMixtureHMM

A hidden Markov model with multivariate Gaussian mixture emissions.

Methods

__init__(*[, n_states, n_components, ...])

Initializes the GaussianMixtureHMM.

aic(X, *[, lengths])

The Akaike information criterion of the model, evaluated with the maximum likelihood of X.

bic(X, *[, lengths])

The Bayesian information criterion of the model, evaluated with the maximum likelihood of X.

fit(X, *[, lengths])

Fit the HMM to the sequences in X, using the Baum—Welch algorithm.

freeze([params])

Freeze the trainable parameters of the HMM, preventing them from be updated during the Baum—Welch algorithm.

score(x, /)

Calculate the log-likelihood of the HMM generating a single observation sequence.

set_state_covars(covars, /)

Set the covariance matrices of the state emission distributions.

set_state_means(means, /)

Set the mean vectors of the state emission distributions.

set_state_start_probs([probs])

Set the initial state probabilities.

set_state_transition_probs([probs])

Set the transition probability matrix.

set_state_weights(weights, /)

Set the component mixture weights of the state emission distributions.

unfreeze([params])

Unfreeze the trainable parameters of the HMM, allowing them to be updated during the Baum—Welch algorithm.

n_params

Number of trainable parameters — requires fit().

class sequentia.models.hmm.variants.GaussianMixtureHMM

A hidden Markov model with multivariate Gaussian mixture emissions.

Examples

Using a GaussianMixtureHMM to learn how to recognize spoken samples of the digit 3.

See load_digits() for more information on the sample dataset used in this example.

import numpy as np
from sequentia.datasets import load_digits
from sequentia.models.hmm import GaussianMixtureHMM

# Seed for reproducible pseudo-randomness
random_state = np.random.RandomState(1)

# Fetch MFCCs of spoken samples for the digit 3
data = load_digits(digits=[3])
train_data, test_data = data.split(test_size=0.2, random_state=random_state)

# Create and train a GaussianMixtureHMM to recognize the digit 3
model = GaussianMixtureHMM(random_state=random_state)
X_train, lengths_train = train_data.X_lengths
model.fit(train_data.X, lengths=train_data.lengths)

# Calculate the log-likelihood of the first test sample being generated by this model
x, y = test_data[0]
model.score(x)
__init__(*, n_states=5, n_components=3, covariance=CovarianceMode.SPHERICAL, topology=TopologyMode.LEFT_RIGHT, random_state=None, hmmlearn_kwargs=None)

Initializes the GaussianMixtureHMM.

Parameters:

  • self (GaussianMixtureHMM) –

  • n_states (int) – Number of states in the Markov chain.

  • n_components (int) – Number of Gaussian components in the mixture emission distribution for each state.

  • covariance (CovarianceMode) – Type of covariance matrix in the mixture emission distribution for each state - see Covariance matrix types.

  • topology (TopologyMode | None) –

    Transition topology of the Markov chain — see Topologies.

    If None, behaves the same as 'ergodic' but with hmmlearn initialization.

  • random_state (int | RandomState | None) – Seed or numpy.random.RandomState object for reproducible pseudo-randomness.

  • hmmlearn_kwargs (dict[str, Any] | None) – Additional key-word arguments provided to the hmmlearn HMM constructor.

Return type:

GaussianMixtureHMM

aic(X, *, lengths=None)

The Akaike information criterion of the model, evaluated with the maximum likelihood of X.

Parameters:

  • self (BaseHMM) –

  • X (ndarray[Any, dtype[float64]] | ndarray[Any, dtype[int64]]) – Sequence(s).

  • lengths (ndarray[Any, dtype[int64]] | None) –

    Lengths of the sequence(s) provided in X.

    • If None, then X is assumed to be a single sequence.

    • len(X) should be equal to sum(lengths).

Returns:

The Akaike information criterion.

Return type:

float

Notes

This method requires a trained model — see fit().

bic(X, *, lengths=None)

The Bayesian information criterion of the model, evaluated with the maximum likelihood of X.

Parameters:

  • self (BaseHMM) –

  • X (ndarray[Any, dtype[float64]] | ndarray[Any, dtype[int64]]) – Sequence(s).

  • lengths (ndarray[Any, dtype[int64]] | None) –

    Lengths of the sequence(s) provided in X.

    • If None, then X is assumed to be a single sequence.

    • len(X) should be equal to sum(lengths).

Returns:

The Bayesian information criterion.

Return type:

float

Notes

This method requires a trained model — see fit().

fit(X, *, lengths=None)

Fit the HMM to the sequences in X, using the Baum—Welch algorithm.

Parameters:

  • self (BaseHMM) –

  • X (ndarray[Any, dtype[float64]] | ndarray[Any, dtype[int64]]) – Sequence(s).

  • lengths (ndarray[Any, dtype[int64]] | None) –

    Lengths of the sequence(s) provided in X.

    • If None, then X is assumed to be a single sequence.

    • len(X) should be equal to sum(lengths).

Returns:

The fitted HMM.

Return type:

BaseHMM

freeze(params=None, /)

Freeze the trainable parameters of the HMM, preventing them from be updated during the Baum—Welch algorithm.

Parameters:

  • self (GaussianMixtureHMM) –

  • params (str | None) –

    A string specifying which parameters to freeze. Can contain a combination of:

    • 's' for initial state probabilities,

    • 't' for transition probabilities,

    • 'm' for emission distribution means,

    • 'c' for emission distribution covariances,

    • 'w' for emission distribution mixture weights.

Return type:

None

See also

unfreeze

Unfreeze the trainable parameters of the HMM, allowing them to be updated during the Baum—Welch algorithm.

score(x, /)

Calculate the log-likelihood of the HMM generating a single observation sequence.

Parameters:
Returns:

The log-likelihood.

Return type:

float

Notes

This method requires a trained model — see fit().

set_state_covars(covars, /)

Set the covariance matrices of the state emission distributions.

If this method is not called, covariance matrices will be initialized by hmmlearn.

Parameters:
Return type:

None

Notes

If used, this method should normally be called before fit().

set_state_means(means, /)

Set the mean vectors of the state emission distributions.

If this method is not called, mean vectors will be initialized by hmmlearn.

Parameters:
Return type:

None

Notes

If used, this method should normally be called before fit().

set_state_start_probs(probs=TransitionMode.RANDOM, /)

Set the initial state probabilities.

If this method is not called, initial state probabilities are initialized depending on the value of topology provided to __init__().

  • If topology was set to 'ergodic', 'left-right' or 'linear', then random probabilities will be assigned according to the topology by calling set_state_start_probs() with probs='random'.

  • If topology was set to None, then initial state probabilities will be initialized by hmmlearn.

Parameters:

  • self (BaseHMM) –

  • probs (ndarray[Any, dtype[float64]] | TransitionMode) –

    Probabilities or probability type to assign as initial state probabilities.

    • If an Array, should be a vector of starting probabilities for each state.

    • If 'uniform', there is an equal probability of starting in any state.

    • If 'random', the vector of initial state probabilities is sampled from a Dirichlet distribution with unit concentration parameters.

Return type:

None

Notes

If used, this method should normally be called before fit().

set_state_transition_probs(probs=TransitionMode.RANDOM, /)

Set the transition probability matrix.

If this method is not called, transition probabilities are initialized depending on the value of topology provided to __init__():

  • If topology was set to 'ergodic', 'left-right' or 'linear', then random probabilities will be assigned according to the topology by calling set_state_transition_probs() with value='random'.

  • If topology was set to None, then initial state probabilities will be initialized by hmmlearn.

Parameters:

  • self (BaseHMM) –

  • probs (ndarray[Any, dtype[float64]] | TransitionMode) –

    Probabilities or probability type to assign as state transition probabilities.

    • If an Array, should be a matrix of probabilities where each row must some to one and represents the probabilities of transitioning out of a state.

    • If 'uniform', for each state there is an equal probability of transitioning to any state permitted by the topology.

    • If 'random', the vector of transition probabilities for each row is sampled from a Dirichlet distribution with unit concentration parameters, according to the shape of the topology.

Return type:

None

Notes

If used, this method should normally be called before fit().

set_state_weights(weights, /)

Set the component mixture weights of the state emission distributions.

If this method is not called, component mixture weights will be initialized by hmmlearn.

Parameters:
Return type:

None

Notes

If used, this method should normally be called before fit().

unfreeze(params=None, /)

Unfreeze the trainable parameters of the HMM, allowing them to be updated during the Baum—Welch algorithm.

Parameters:

  • self (GaussianMixtureHMM) –

  • params (str | None) –

    A string specifying which parameters to unfreeze. Can contain a combination of:

    • 's' for initial state probabilities,

    • 't' for transition probabilities,

    • 'm' for emission distribution means,

    • 'c' for emission distribution covariances,

    • 'w' for emission distribution mixture weights.

Return type:

None

See also

freeze

Freeze the trainable parameters of the HMM, preventing them from be updated during the Baum—Welch algorithm.

covariance: CovarianceMode

Type of covariance matrix in the emission model mixture distribution for each state.

hmmlearn_kwargs: dict[str, Any]

Additional key-word arguments provided to the hmmlearn HMM constructor.

model: BaseHMM

Underlying HMM object from hmmlearn — only set after fit().

n_components: int

Number of Gaussian components in the emission model mixture distribution for each state.

property n_params: int

Number of trainable parameters — requires fit().

n_states: int

Number of states in the Markov chain.

random_state: int | RandomState | None

Seed or numpy.random.RandomState object for reproducible pseudo-randomness.

topology: TopologyMode

Transition topology of the Markov chain — see Topologies.